A note on the purpose and pedagogy of the course
by Dag Wedelin
The course originated from the observation that students on some programs (I first considered the D and IT-programs at Chalmers), encounter a large distance between the mathematics courses and the other courses in the curriculum. In many engineering programs mathematics is studied in parallel with engineering courses where similar mathematics is immediately applied. At D and IT instead programming and other subjects are given side by side with the mathematics courses, and the link to mathematics is not so clear. Additionally, it is not uncommon that students have chosen in particular the IT program partly because they see mathematics as a topic on the side in their education. The result is that many D and IT students never understand the many links that actually exist, and also never learn how they can actively use mathematics in their profession.
Since it is difficult to predict in which areas different D and IT students will come to work, my solution was to suggest and create a broad course in mathematical modelling and problem solving, rather than in some particular engineering subject. The course is at present compulsory in the second year of the IT-program. D students often select the course in their third year.
In simple terms, the course can be described as 1) adding a critical missing piece of knowledge (mathematical models), and 2) help the students to develop the skills to fully use their mathematical knowledge (structured problem solving). This can be illustrated in relation to Bloom's taxonomy:
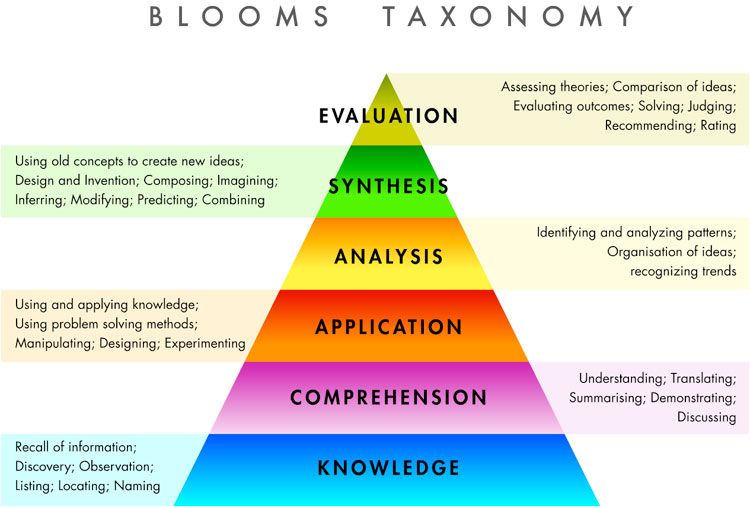
Image from juliaec.wordpress.com
As a result, this course together with the mathematics the student already knows, gives the student a considerably more complete set of tools to tackle unknown problems in new situations.
Some key pedagogical aspects of the course are:
- The course is defined by problems, designed with a general aim to consider situations that the student may encounter in the future.
- A broad range of non-trivial problems span over different kinds of applications and approaches. Many exercises are formulated so that solving them becomes a form of exploration.
- Problem solving strategies are actively taught.
- Supervision is done interactively, mainly by asking questions. Personal contact between students and teachers is prioritized.
- Feedback is regularly given in different ways during the course.
When comparing the pedagogical approach to other courses, one might say that the course represents an intermediate step between straightforward knowledge oriented courses, and project courses. Compared to traditional courses this course has a much higher emphasis on methods and skills for handling the unknown. Compared to project courses, the student will encounter a wide range of problems and approaches, and will learn to make appropriate distinctions and choices. So the controlled setting of this course, with a large number of varied problems that the teachers know very well, can be seen to prepare the student for projects and other more independent work.
Dag Wedelin
