Optimization models
The following modelling problems will train your ability to model situations as optimization problems. The general approach of setting up of variables and equations is useful for a wide range of modelling and engineering problems, and not just for optimization.
Some of the problems here are very small so that you shall be able to work with them manually. However, powerful mathematical optimization algorithms can solve problems with thousands and sometimes even millions of variables.
Problem 5 is a bit different from the other problems since it involves several agents that individually try to optimize their own outcome, rather than a common goal.
Mathematica code for the introductory lecture examples
OPTIMAL CAN PROBLEM
NMaximize[{Pi r^2 h, 2 Pi r h + 2 Pi r^2 == 1, r >= 0, h >= 0},{r, h}]
SIMPLE ASSIGNMENT PROBLEM
NMinimize[
{1 x11 + 3 x12 + 5 x13 + 1 x14 + 4 x21 + 5 x22 + 3 x23 + 2 x24 +
7 x31 + 4 x32 + 6 x33 + 9 x34 + 8 x41 + 4 x42 + 7 x43 + 3 x44,
x11 + x12 + x13 + x14 == 1,
x21 + x22 + x23 + x24 == 1,
x31 + x32 + x33 + x34 == 1,
x41 + x42 + x43 + x44 == 1,
x11 + x21 + x31 + x41 == 1,
x12 + x22 + x32 + x42 == 1,
x13 + x23 + x33 + x43 == 1,
x14 + x24 + x34 + x44 == 1,
0 <= x11 <= 1, 0 <= x12 <= 1, 0 <= x13 <= 1, 0 <= x14 <= 1,
0 <= x21 <= 1, 0 <= x22 <= 1, 0 <= x23 <= 1, 0 <= x24 <= 1,
0 <= x31 <= 1, 0 <= x32 <= 1, 0 <= x33 <= 1, 0 <= x34 <= 1,
0 <= x41 <= 1, 0 <= x42 <= 1, 0 <= x43 <= 1, 0 <= x44 <= 1},
{x11, x12, x13, x14, x21, x22, x23, x24, x31, x32, x33, x34, x41,
x42, x43, x44}
]
The Problems
(CHOCOLATE FACTORY PROBLEM) The family business Fluffy-Fudge-Chocolates are famous for their Fluffy-Fudge chocolate bar, which they have been selling for the last fifty years in their area and around. However, they are struggling with volume and profitability - in the last years the price has increased because of higher fixed costs. They are now considering to invest in a new machine that would make packing fully automatic, thereby improving profitability and possibly saving the business. The company is currently producing a little more than 80000 chocolate bars a year. The annual revenue is about 1.3 Mkr, and they made a marginal loss last year of about 40000 kr.
They think that the new machine - at a cost of about 450000 kr - could maybe reduce the variable production costs from about 5 kr to 3 kr per chocolate bar. They are better with chocolate than with numbers, so they hired you as their mathematical consultant in the hope of a solid analysis before any decision.
They don't have very systematic or consistent data, the most reliable figures seem to be in their home city during the last few years (the overall trend in total sales appears to be similar):
year quantity unit price 2016 10300 15 kr 2017 8100 17 kr 2018 7400 18 kr You will meet the owners next week to present a preliminary analysis and suggestions based on the information you currently have. What will you say?
-
(EMERGENCY CARE PROBLEM) The following problem is a facility location problem. A city wishes to make a long term study to decide where to best locate emergency care. The city has been partitioned into regions, and it has been decided that an emergency care site can acceptably service regions of the city which are within a driving distance of 8 minutes. The goal is to choose a set of stations at minimum cost. There are seven regions to cover, and six potential sites have been identified.
Distances in minutes between regions and potential sites:
Site # 1 2 3 4 5 6 Region 1 15 3 12 5 17 20 Region 2 12 9 13 16 3 4 Region 3 13 16 9 4 7 11 Region 4 3 22 12 5 16 18 Region 5 4 7 6 22 5 14 Region 6 8 10 5 16 13 5 Region 7 13 10 5 6 13 21 The cost for locating emergency care on the respective sites:
Cost Site 1 710 000 Site 2 610 000 Site 3 650 000 Site 4 910 000 Site 5 720 000 Site 6 570 000 -
Model this problem mathematically by defining variables, constraints and an objective function. To get started, you can simply begin to define some variables, write some equations and see what you get along the way. Note that in this step you are not solving the problem, just defining it. Hint: think about what I said in the lecture about how to define the variables!
If the objective function and constraints that you found in part a are not all linear, then try to model the function again, this time as a linear programming problem (i.e. objective function and constraints all linear).
Now try to solve your model by using the Mathematica function NMinimize. We know that the values of the variables must be integers but, just to see what happens, try to solve it with continuous variables first. What conclusions can you draw from the solution you obtain?
Then solve the original integer problem, by using the Integers keyword in Mathemtica. (See the section Scope in the documentation on the NMinimize function.) Where should emergency care facilities be built?
Ask yourself if this is the only way to handle this problem? For example, in this problem we assumed that we should have a maximum number of minutes from each region of the city. Is this the only way to think about this? If you can, elaborate on any idea you might have.
Note that while this problem only has a small number of variables and therefore can be solved by brute force combinatorial search, this would be useless for larger problems. For larger problems the more mathematical approach is much more powerful.
(COMMUNICATIONS NETWORK PROBLEM) A small telecom operator wishes to connect the two hubs A and F in a part of their network. The network they can use for this purpose consists of links between the locations A-F with the following capacities in Mbit/s.
AB
16
AC
48
BD
32
BE
8
CD
8
CE
32
DF
64
EF
16
The operator now wishes to determine
how to route as much communication as possible from A to F, and what the maximum capacity is. The idea is to use all links as much as possible at the same time. Model this problem mathematically and solve with Mathematica. Hint: when you define the variables and write your equations, do not worry about the fact that you do not yet know the solution. This is the idea with variables, that you can write equations/inequalities with them without knowing their values. Only at the end when all equations/inequalities are written we need to think about actually solving the problem and getting the values.How would the capacity be reduced if link BD breaks? Use Mathematica to find the solution.
If the currently needed capacity is about 35 Mbit/s, is it possible to eliminate some links entirely? Use Mathematica to find a solution.
(SHORTEST PATH AS LP PROBLEM) (This problem is optional, but please try to understand the problem even if you decide not to attempt to solve it.) Describe how the shortest path problem can be modelled as a linear programming problem.
Hint: Model the problem as a flow from A to B. For each link you can have a cost per unit of flow, and you can also set bounds on the flow. In what sense can the shortest path problem be said to be a linear programming problem and vice versa? What if you are interested in the shortest paths from node A to all other nodes? This problem is a bit more abstract than the others.
(BRIDGE PROBLEM) Consider the road network below. The figure illustrates the roads between two larger cities along a river. Roads B and C are large roads and have a fixed travel time of about 30 minutes independently of the traffic load. The roads A and D are mountain roads and the travel time is estimated to about 10+x minutes where x is the traffic intensity in cars per minute (in one direction). During rush hours the total traffic between the cities in either direction s is about 20 cars per minute.
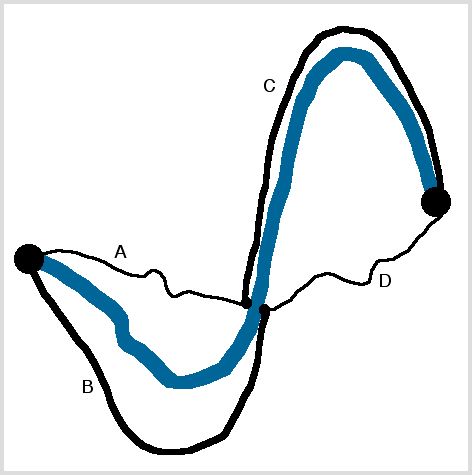
- Assuming that every individual tries to optimize his/her own travel time, what will be the travel time during rush hours? Motivate your answer. Hint: consider if all individual decisions of drivers could eventually lead to some equilibrium state with constant traffic flows?
- In order to improve traffic flow it is decided to build a bridge over the river between the two small communities. The travel time over the bridge is about 1 minute independently of the traffic volumes we are considering. Again, assuming that every individual tries to optimize his/her own travel time, what will be the new travel time between the large cities? Motivate your answer, discuss the result and draw qualitative conclusions.
SELF-CHECK
- Have you answered all questions to the best of your ability?
- Is all the required information on the front page, is the file name correct etc.? (See here)
- Anything else you can easily check? (details, terminology, arguments, clearly stated answers etc.?)
Do not submit an incomplete module! We are available to help you, and you can receive a short extension if you contact us.
-
